The end behavior of a function tells us what happens at the tails. Endbehaviorfxlnx-5 endbehaviorfxfrac1x2 endbehavioryfracxx2-6x8 endbehaviorfxsqrtx3.

Determining End Behavior By Openstax Page 4 13 Jobilize Com Polynomial Functions Polynomials Precalculus
Normally you say write this like this.

. End behavior describes what the output y or f x does as x grows infinitely small to the left x - or as x grows infinitely large to the right x. As we have already learned the behavior of a graph of a polynomial function of the form. X goes to negative and positive infinity.
Identify the end behavior of the function by looking at the leading term. The table below shows the end behavior of power functions in the form latexfleftxrightkxnlatex where latexnlatex is a non-negative integer depending on the power and the constant. The end behavior of the functions are all going down at both ends.
In this video we learn the Algebra 2 way of describing those little arrows yo. The behavior of the graph of a function as the input values get very small latexxto -inftylatex and get very large latexxto inftylatex is referred to as the end behavior of the function. F f will behave at the end of the x-axis.
Graph 1x -10 10 -5 5. The end behavior of a function describes the behavior of the graph of the function at the ends of the -axis. To determine its end behavior look at the leading term of the polynomial function.
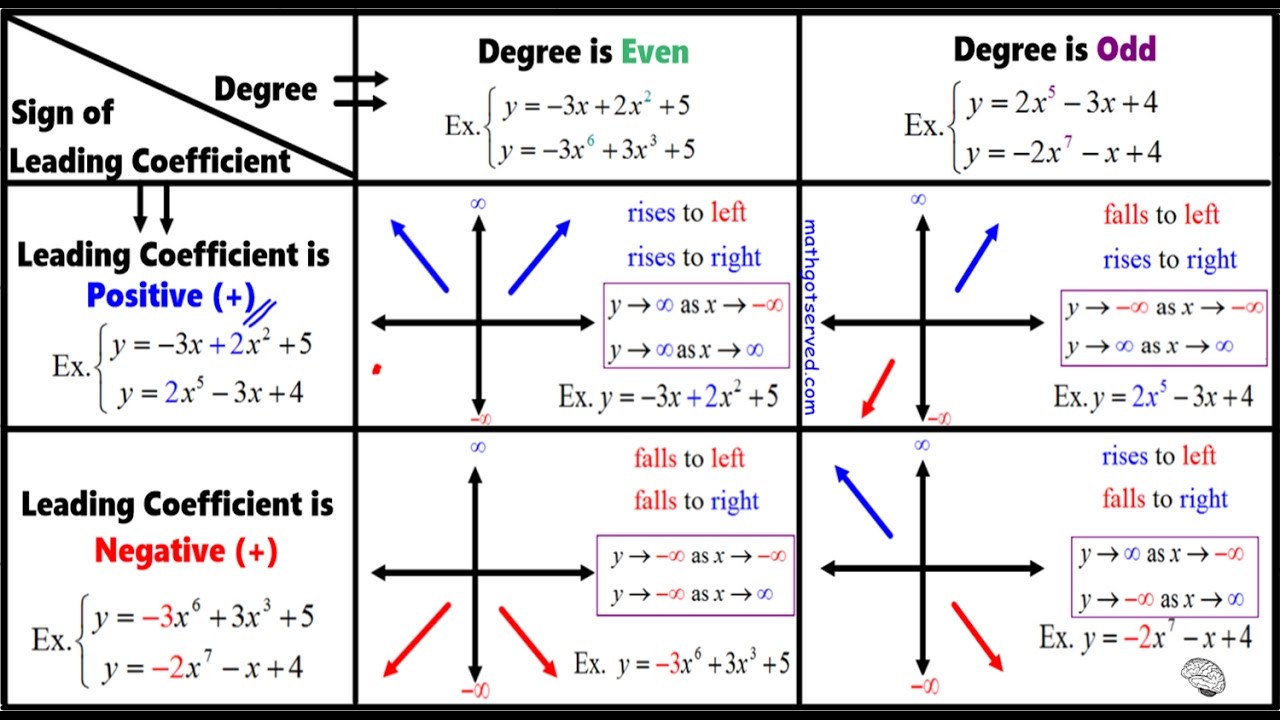
This is determined by the degree and the leading coefficient of a polynomial function. F x anxn an1xn1 a1xa0 f x a n x n a n 1 x n 1. The end behavior of a function is the behavior of the graph of the function f x as x approaches positive infinity or negative infinity.
As x heads to infinity is just saying as you keep going right on the graph and x going to negative infinity is. There are three main types of end behavior. As x heads to infinity and as x heads to negative infinity.
A 1 x a 0. We can use words or symbols to describe end behavior. Y f x y fleft x right y f x it can be observed that as the value of x approaches.
Recall that we call this behavior the end behavior of a function. Where P is a nonzero constant commonly referred to as the fundamental period. F x -x2 2x 3.
Will either ultimately rise or fall as x increases without bound and will either rise or fall as x decreases without bound. For example in case of y f x 1 x as x f x 0. The end behavior of a function is the behavior of the graph of the function f x as x approaches positive infinity or negative infinity.
In other words the end behavior of a function describes the trend of the graph if we look to the right end of the -axis as approaches and to the left end of the -axis as approaches. G x -x4 x3 x2. The same is true for very small inputs say 100 or 1000.
End behavior describes where a function is going at the extremes of the x-axis. Where the independent variable ie. Because the power of the leading term is the highest that term will grow significantly faster than the other terms as x gets very large or very small so its behavior will dominate the graph.
For example in case of y f x 1 x as x f x 0. This is because the leading coefficient is. This example provides two examples of how to describe the end behavior and long run behavior of a functionSite.
As x grows infinitely small if the outputs are decreasing we say this is down. When the leading term is an odd. Graph 1x -10 10 -5 5.
The end behavior of the function is determined by the degree and the leading coefficient of the function. End behavior is just how the graph behaves far left and far right. The end behavior of a function is a way of classifying what happens when x gets close to infinity or the right side of the graph and what happens when x.
As x grows infinitely small if the outputs are increasing we say this is up left. We can use words or symbols to describe end behavior. For example the cosine and sine functions ie.
This is determined by the degree and the leading coefficient of a polynomial function. Limit of the function goes to infinity either positive or negative as x. As we pointed out when discussing quadratic equations when the leading term of a polynomial function anxn a n x n is an even power function as x increases or decreases without bound f x f x increases without bound.
For any polynomial the end behavior of the polynomial will match the end behavior of the term of. If we look at the graph of the function lets say. A periodic function is basically a function that repeats after certain gap like waves.
The parity of the exponent and the sign of the coefficient determines the end behavior of the function as a whole. H x -x8 - 3. F x cos x and f x sin x are both periodic since their graph is wavelike and it repeats.
Polynomials Teaching Mathematics

Graphing And Finding Roots Of Polynomial Functions Math Hints Teaching Algebra School Algebra High School Math Classroom

The Agony And Dx Dt End Behavior Of Polynomial Functions Studying Math Teaching Algebra Math Formulas

End Behavior Of A Polynomial Function A Graphing Calculator Investigation Polynomial Functions Polynomials Quadratics
0 Comments